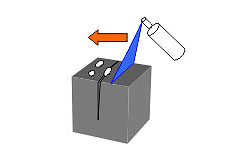
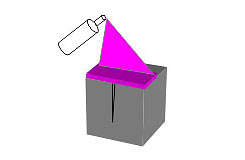
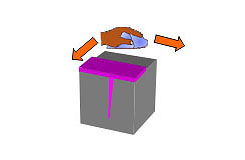
Микроструктурные свойства полярных пенетрантов
Известно, что при определенных условиях полярная жидкость течет в микрокапилляре медленнее, чем неполярная в том же канале с тем же значением сдвиговой вязкости и при том же градиенте давления. Условия эти определяются степенью полярности жидкости и поперечным размером канала R (радиусом поры или расстоянием между стенками трещины). С увеличением полярности жидкости и уменьшением R возрастает отклонение профиля скорости от классического, рассчитанного для ньютоновской жидкости.
Например, экспериментально измеренная эффективная вязкость воды в микрокапилляре радиусом R = 0,03-0,05 мкм на 40% выше, а в тонкопористых стеклах со средним радиусом пор от 20 до 100А – на 50-100% выше ее табличного значения для данной температуры. Отметим, что при R > 0,5 мкм гидродинамика воды, являющейся сильно полярной жидкостью, достаточно хорошо описывается уравнениями классической модели ньютоновской жидкости.
Описать столь необычные экспериментальные результаты, полученные при исследовании сдвиговых течений полярных жидкостей в микрокапиллярах, можно в рамках моделей жидкости, учитывающих наличие не только сдвиговых, но и моментных напряжений. Причина повышения эффективной вязкости полярной жидкости в микрокапилляре состоит в том, что диссипация энергии, требуемой для перемещения жидкости, определяется не только классическим трением за счет сдвиговых напряжений, но и вращательным трением вследствие наличия моментных напряжений между ассоциатами полярной жидкости.
Реологические свойства воды, являющейся типичной ньютоновской жидкостью при ее течении в каналах с R > 0,5 мкм, в микрокапиллярах меньшего поперечного размера становятся принципиально иными. В этом случае связь между скоростью деформаций и тензором напряжений уже не является линейной, а в реологическом уравнении состояния появляются моментные напряжения и, соответственно, дополнительные реологические константы, фигурирующие в целом ряде теорий жидкостей с внутренними степенями свободы.
Строго говоря, четкой границы между течением, описываемым классическим уравнением Навье-Стокса, и течением, которое необходимо описывать более сложными уравнениями, не существует. Например, при впитывании воды в капилляр радиусом R = 2 · 10-6 м моментные напряжения существуют, но обоснованно считаются пренебрежимо малыми. С уменьшением радиуса капилляра вклад внутренних микровращений ассоциатов жидкости в величину диссипируемой энергии растет. В результате эффективная вязкость жидкости, например, пенетранта в микротрещине, может на 50-70% превышать значение ее сдвиговой вязкости.
Таким образом, подбирая более полярный пенетрант, можно существенно увеличить степень заполнения им полости дефекта за счет пленочного течения при двустороннем заполнении канала. Это, в свою очередь, приводит к увеличению чувствительности капиллярной дефектоскопии, поскольку, чем больше пенетранта попадает в полость дефекта, тем больший по площади индикаторный след дефекта образуется при последующем проявлении после нанесения проявителя.
Но, с другой стороны, именно полярность пенетранта может быть причиной значительного увеличения его эффективной вязкости при течении в микрокапилляре, замедляя процесс пропитки дефекта и, соответственно, существенно снижая производительность капиллярной дефектоскопии.